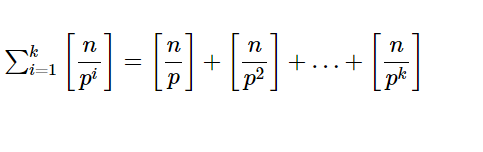ここで勉強すれば数学検定１級の壁は超えられるか。

[math]2018n\equiv 2\left( mod1000\right)[/math]

 

 

 この式は

 

[math]18n\equiv 2\left( mod1000\right)[/math]

 

 
 と同じになるので

 
 

[math]18n=1000y+2[/math]

 

の方程式を考える。 
 

 

上記の等式が成り立つｎとｙを探す。
 
 

ｙ＝１のとき　　１００２÷１８＝５５…１２
 
成り立たない 

 

ｙ＝２のとき　　２００２÷１８＝１１１…４
 
成り立たない

 

ｙ＝３のとき　　３００２÷１８＝１６６…１４
 
成り立たない
 

ｙ＝４のとき　　４００２÷１８＝２２２…６
 
成り立たない

 

ｙ＝５のとき　　５００２÷１８＝２７７…１６
 
成り立たない

 

ｙ＝６のとき　　６００２÷１８＝３３３…８
 
成り立たない

 

ｙ＝７のとき　　７００２÷１８＝３８９…０
 
成り立つ

 

 

 

したがってｙ＝７　ｎ＝３８９のとき18ｎ=1000y+2が成り立つ。
 
 

ｎの最小値は３８９になる。

 

 

 

 

 
 

別解１

 

[math]18n=1000y+2\Rightarrow 9n=500y+1[/math]

 

 

9n=501.1001.1501.2001.2501.3001.3501.4001.4501.5001,5501,・・・・・・

 

 

 

９も倍数は各位の数の和が９の倍数なので、上記の数の中で、最小の９の倍数は３５０１になる。

 

 

 

９ｎ＝３５０１より　　　　ｎ＝３８９

 

 

答え　　　３８９

 

 

 

 

 

 

別解２

 

 

前記の　９ｎー５００ｙ＝１・・・①（n，yは整数）

 

 

９と５００はお互いに素なので、①の不定方程式は解が大きいので、ユークリッド互除法で解く。

 

 

CGD(９，５００）＝（９，５００－５５×９）＝（９，５）＝（９－１×５，５）＝（４，５）＝（４，１）＝１

 

 

上の過程をa＝９，ｂ＝５００として行うと

 

 

 

（a，ｂ）＝（a，ｂ－５５a）＝（aーｂ＋５５a，ｂ－５５a）

 

＝（５６aーｂ，ｂ－５５a）＝（５６aーｂ，－５５aー５６a＋２ｂ）

 

＝（５６aーｂ，ー１１１a＋２ｂ）＝（４，１）

 

 

したがって、ー１１１a＋２ｂ＝１　

 

 

 

式変形して

 

 

（－１１１）×aー（－２）×ｂ＝１となる。

 

 

よって　　ｎ＝－１１１＋５００ｋ（ｋは整数）・・・②

 

 

　　　　　ｙ＝－２＋９ｍ（ｍは整数）

 

 

 

求めるｎは正の整数の最小値なので、ｋ＝１を②式に代入して

 

 

ｎ＝－１１１＋５００＝３８９

 

 

 

答え　　　３８９