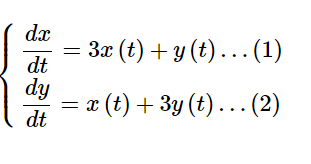微分方程式１９の解説

[math]y\left( 0\right) =-3[/math]のとき次の微分方程式を解きなさい。

[math]\dfrac{dy}{dx}=\left( y-x\right) ^{2}[/math]

[math]y-x=u[/math]とおいて両辺をⅹで微分すると

[math]\dfrac{dy}{dx}-1=\dfrac{du}{dx}[/math]となり、上の微分方程式は

[math]\dfrac{du}{dx}=u^{2}-1[/math]となる。

[math]\dfrac{1}{u^{2}-1}du=dx[/math]を解いて

[math]\int \dfrac{1}{2}\left\{ \dfrac{1}{u-1}-\dfrac{1}{u+1}\right\} du=\int dx[/math]

[math]log\dfrac{u-1}{u+1}=2x+c[/math]　　ｃは積分定数

[math]\dfrac{u-1}{u+1}=\dfrac{y-x-1}{y-x+1}=Ae^{2x}[/math]・・・（１）

Aは積分定数

[math]y\left( 0\right) =-3[/math]より積分定数[math]A=\dfrac{-3-0-1}{-3-0+1}=2[/math]

（１）より

[math]y-x-1=2e^{2x}\left( y-x+1\right)[/math]

[math]\left( 1-2e^{2x}\right) y=\left( 1-2e^{2x}\right) x+1+2e^{2x}[/math]

[math]y=x+\dfrac{1+2e^{2x}}{1-2e^{2x}}[/math]・・・答