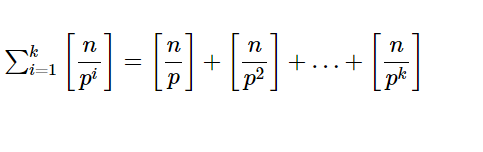ここで勉強すれば数学検定１級の壁は超えられるか。

[math]15^{2010}[/math]を１２８で割った余りを正の数で求める。

[math]1 5^{2010}=\left( 16-1\right) ^{2010}=\left( 2^{4}-1\right) ^{2010}[/math]

二項定理で展開すると

[math]\left( 2^{4}\right) ^{2010}+2010\cdot \left( 2^{4}\right) ^{2009}\cdot \left( -1\right)+\dfrac {2010\times 2009}{2\times 1}\cdot \left( 2^{4}\right) ^{2008}\cdot \left( -1\right) ^{2}+\ldots+2010\cdot \left( 2^{4}\right) \cdot \left( -1\right) ^{2009}+\left( -1\right) ^{2010}[/math]

したがって

[math]15^{2010}\equiv 2010\cdot \left( 2^{4}\right) \left( -1\right) ^{2009}+\left( -1\right) ^{2010} \left( mod2^{7}\right)[/math]　

[math]\equiv -\left( 251\cdot 2^{3}+2\right) \cdot \left( 2^{4}\right) +1[/math]

[math]\equiv -32+1\equiv 97\left( mod128\right)[/math]　

答え　　９７