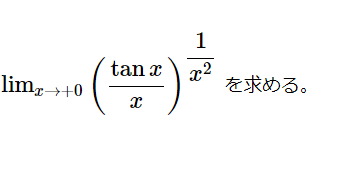ここで勉強すれば数学検定１級の壁は超えられるか。

 

 

[math]a_{n+2}=\left( n+1\right) \left( a_{n+1}+ a_{n}\right)   ,a_{1}=0,a_{2}=1[/math]

 

 

 

（１）

 

[math]b_{n}=a_{n+1}-\left( n+1\right) a_{n}[/math]

 

 

より

 

 

[math]b_{n+1}+b_{n}=a_{n+2}-\left( n+1\right) a_{n+1}+a_{n+1}-\left( n+1\right) a_{n}[/math]

 

 

 

[math]=a_{n+2}-\left( n+1\right) a_{n+1}-\left( n+1\right) a_{n}[/math]

 

 

[math]=a_{n+2}-\left( n+1\right) \left( a_{n+1}+a_{n}\right) =0[/math]

 

 

したがって

 

 

[math]b_{1}=1,b_{n+1}=-b_{n}\rightarrow b_{n}=\left( -1\right) ^{n-1}[/math]

 

 

[math]b_{n}=\left( -1\right) ^{n-1}[/math]・・・（１）の答え

 

 

 

（２）

 

 

[math]b_{n}=a_{n+1}-\left( n+1\right) a_{n}=\left( -1\right) ^{n-1}[/math]

 

 

 

両辺を[math]\left( n+1\right) ![/math]で割る。

 

 

 

[math]\dfrac {a_{n+1}}{\left( n+1\right) !}-\dfrac {a_{n}}{n!}=\dfrac {\left( -1\right) ^{n-1}}{\left( n+1\right) !}[/math]

 

 

したがって

 

 

 

[math]\dfrac {a_{n}}{n!}=\dfrac {a_{1}}{1!}+\sum ^{n-1}_{k=1}\dfrac {\left( -1\right) ^{k+1}}{\left( k+1\right) !}[/math]

 

 

 

[math]=0+\sum ^{n}_{k=2}\dfrac {\left( -1\right) ^{k}}{k!}=\dfrac {\left( -1\right) ^{0}}{0!}+\dfrac {\left( -1\right) ^{1}}{1!}+\sum ^{n}_{k=2}\dfrac {\left( -1\right) ^{k}}{k!}=\sum ^{n}_{k=0}\dfrac {\left( -1\right) ^{k}}{k!}[/math]

 

 

したがって

 

[math]\lim _{n\rightarrow \infty }\dfrac {a_{n}}{n!}=\sum ^{\infty }_{k=0}\dfrac {\left( -1\right) ^{k}}{k!}=e^{-1}[/math]

 

 

 

 

[math]\dfrac {1}{e}[/math]・・・（２）の答え