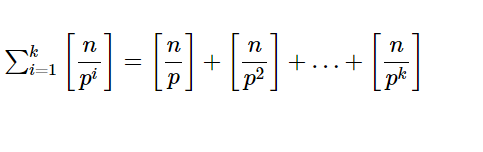ここで勉強すれば数学検定１級の壁は超えられるか。

[math]\dfrac {1}{2+\dfrac {1}{3+\dfrac {1}{2+\dfrac {1}{3+\ldots }}}}[/math]

２と３の数の部分の繰り返しより

[math]2+\dfrac {1}{3+\ldots }[/math]　　の極限値と上の式の極限値（ｍとおく）と一致するので

[math]\dfrac {1}{2+\dfrac {1}{3+m}}=m[/math]　　　　　の方程式を考える。

[math]\dfrac {1}{\dfrac {6+2m+1}{3+m}}=\dfrac {m+3}{2m+7}=m[/math]となる。

[math]\begin{aligned}2m^{2}+6m-3=0\\ m=\dfrac {-3\pm \sqrt {15}}{2}\end{aligned}[/math]

０＜ｍ＜１の条件より

[math]\begin{aligned}\sqrt {9} <\sqrt {15} <\sqrt {16}\\ 3 <\sqrt {15} <4\end{aligned}[/math]

だから

[math]m=\dfrac {-3+\sqrt {15}}{2}[/math]