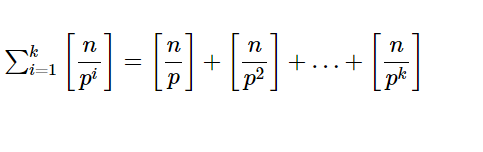ここで勉強すれば数学検定１級の壁は超えられるか。
MENU
数学検定１級の壁 TOP > 数検1級の整数論 > 整数論９の解説
整数論９の解説
[math]21x\equiv 28\left( mod91\right)[/math]
ｘを求める。
合同式を７で割る。
[math]3x\equiv 4\left( mod13\right)[/math]
３ｘ＝１３ｋ＋４ （ｋは整数）
この式を満たすｘを探す。
１から調べていくと、ｘ＝１０のときにｋ＝２で成立する。
３と１３は互いに素であるから
１０から１３ずつ加えていけばよい。
答え・・・１０，２３，３６，４９，６２，７５，８８
同じカテゴリー「数検1級の整数論」の一覧
最高累乗指数(整数１６）
実数ｘに対して[math]\left[ x\right][/math] はｘを超えない最大整数を表す。 n を自然数とする。 n！に含まれる素因数 pの最高累乗指数は &n […]
Copyright© 2024 数学検定１級の壁
