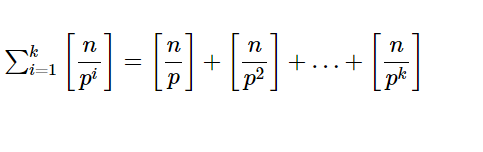ここで勉強すれば数学検定1級の壁は超えられるか。
最高累乗指数(整数16)
実数xに対して[math]\left[ x\right][/math] はxを超えない最大整数を表す。
n を自然数とする。 n!に含まれる素因数 pの最高累乗指数は
[math]p^{k}\leqq n <p^{k+1}[/math]とすると
n!の因数1,2,3,・・・,nの中で pの倍数
[math]p,2p,3p,\ldots ,\left[ \dfrac{n}{\rho }\right] p[/math]の[math]\left[ \dfrac{n}{p}\right][/math]個
であるから[math]\left[ \dfrac{n}{p}\right][/math]回で割り切れる。
次に
[math]p^{2},2p^{2},3p^{2},\ldots \left[ \dfrac{n}{p^{2}}\right] p^{2}[/math]だから
[math]\left[ \dfrac{n}{p^{2}}\right][/math]回で割り切れる。
以下同様にカウントして
[math]\sum ^{k}_{i=1}\left[ \dfrac{n}{p^{i}}\right] =\left[ \dfrac{n}{p}\right] +\left[ \dfrac{n}{p^{2}}\right] +\ldots +\left[ \dfrac{n}{p^{k}}\right][/math]
問題
100!を10進法で表記すれば、末尾に0がいくつ並ぶことになるか。
100!の中に因数として含まれる2と5の個数は明らかに2の方が圧倒的に多い。だから、この因数5の個数が10進法で表記された100!の末尾に並ぶ0の個数に等しい。
100!の中にある因数5はの個数は求める。
素数5の最大累乗指数を求めると
[math]\left[ \dfrac{100}{5}\right] +\left[ \dfrac{100}{5^{2}}\right] =20+4= 24[/math]
答え 24個
同じカテゴリー「数検1級の整数論」の一覧
最高累乗指数(整数16)
実数xに対して[math]\left[ x\right][/math] はxを超えない最大整数を表す。 n を自然数とする。 n!に含まれる素因数 pの最高累乗指数は &n […]