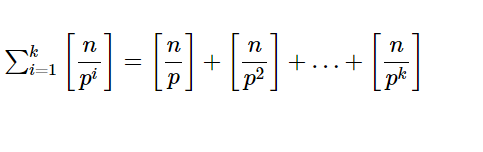ここで勉強すれば数学検定1級の壁は超えられるか。
整数論4の解説 (解と係数の関係)
[math]\left( a+b\right) ^{3}=a^{3}+3ab\left( a+b\right) +b^{3}[/math]の公式を使って計算する。
[math]\sqrt [3] {-5+2\sqrt {13}}+\sqrt [3] {-5-2\sqrt {13}}=x[/math]とおくと
[math]x^{3}=\left( -5+2\sqrt {13}\right) +3\sqrt [3] {\left( 25-52\right) }x+\left( -5-2\sqrt {13}\right)[/math]
したがって
[math]x^{3}=-10+3\sqrt [3] {-27}x[/math]になる、
[math]x^{3}+9x+10=0[/math]より
[math]\left( x+1\right) \left( x^{2}-x-10\right)=0[/math]
xは実数なのでx=-1になる。
また、
[math]\sqrt [3] {-5+2\sqrt {13}}\sqrt [3] {-5-2\sqrt {13}}=-3[/math]
解と係数の関係より次の二次方程式が導かれる。
[math]\begin{aligned}\left( x-\sqrt [3] {-5+2\sqrt {13}}\right) \left( x-\sqrt [3] {-5-2\sqrt {13}}\right) \\ =x^{2}+x-3=0\end{aligned}[/math]
[math]x=\dfrac {-1\pm \sqrt {13}}{2}[/math] この2つの解の大きい方が答えになる。
[math]x=\dfrac {-1+\sqrt {13}}{2}[/math]・・・答え
同じカテゴリー「数検1級の整数論」の一覧
最高累乗指数(整数16)
実数xに対して[math]\left[ x\right][/math] はxを超えない最大整数を表す。 n を自然数とする。 n!に含まれる素因数 pの最高累乗指数は &n […]