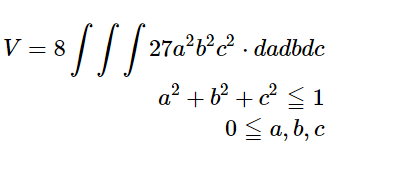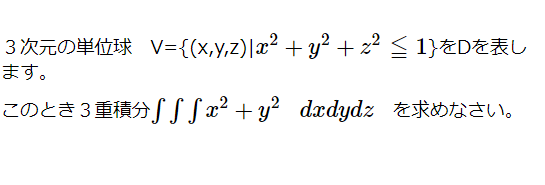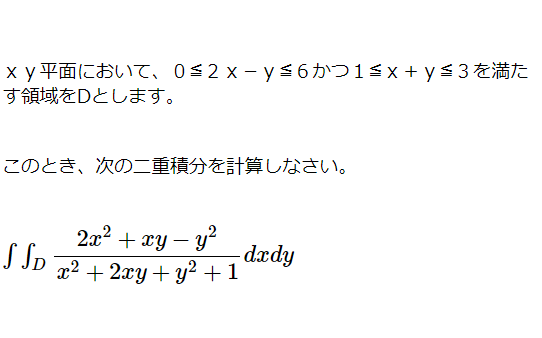ここで勉強すれば数学検定1級の壁は超えられるか。
重積分7の解説

[math]\int ^{3}_{0}dy\int ^{\sqrt {\dfrac {y}{3}}}_{0}\log _{e}\left( x^{3}-3x+3\right) dx[/math]
を求める。
積分領域Dは
[math]0\leqq x\leqq \sqrt {\dfrac {y}{3}}\Rightarrow 0\leqq x^{2}\leqq \dfrac {y}{3}[/math]
[math]\Rightarrow 0\leqq 3x^{2}\leqq y\Rightarrow 3x^{2}\leqq y\leqq 1\times 3[/math]

[math]\int ^{3}_{0}dy\int ^{\sqrt {\dfrac {y}{3}}}_{0}\log _{e}\left( x^{3}-3x+3\right) dx[/math]
[math]=\int ^{1}_{0}dx\int ^{3}_{3x^{2}}\log _{e}\left( x^{3}-3x+3\right) dy[/math]
[math]=\int ^{1}_{0}\left( 3-3x^{2}\right) \log _{e}\left( x^{3}-3x+3\right) dx[/math]
[math]=\int ^{1}_{0}\left( -x^{3}+3x-3\right) '\log _{e}\left( x^{3}-3x+3\right)[/math]
部分積分をすると
[math]=-\left[ \left( x^{3}-3x+3\right) \cdot \log _{e}\left( x^{3}-3x+3\right) \right] ^{1}_{0}+\int ^{1}_{0}\dfrac {3x^{2}-3}{x^{3}-3x+3} \cdot ( x^{3}-3x+3)dx[/math]
[math]=3\log _{e}3+\left[ x^{3}-3x\right] ^{1}_{0}=3\log _{e}3-2[/math]・・・答え
同じカテゴリー「数検1級の重積分」の一覧
極座標に変換して体積を求める。(重積分15)
[math]x^{\dfrac {2}{3}}+y^{\dfrac {2}{3}}+z^{\dfrac {2}{3}}\leqq 1[/math]の領域の体積を求める。 & […]
重積分14の解説(三角関数の2重積分)
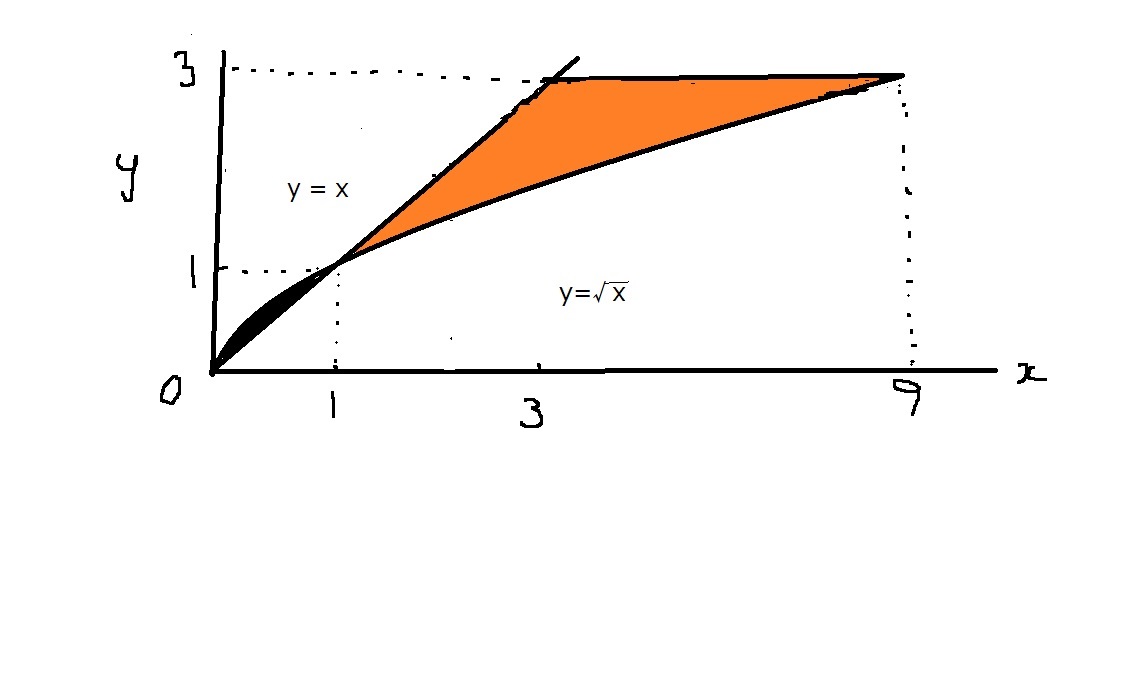
重積分 予想問題 [math]D=\left\{ \left( x,y\right) \left| \right| y\leqq x\leqq y^{2},1 […]
重積分13の解説 (式に絶対値がはいっている2重積分)
平面上の領域D{(x,y)| 0≦x≦1,0≦y≦1 }のとき、 [math]\int \int _{D}\left| x-y\right| ^{-\dfrac {2}{3 […]
重積分12の解説 (円筒座標変換による重積分)
3次元の単位球 V={(x,y,z)|[math]x^{2}+y^{2}+z^{2}\leqq 1[/math]}をDを表します。 このとき3重積分[math]\int \int \in […]
変数変換の二重積分(重積分11)
xy平面において、0≦2x-y≦6かつ1≦x+y≦3を満たす領域をDとしたとき、 [math]\int \int _{D}\dfrac {2x^{2}+xy- […]