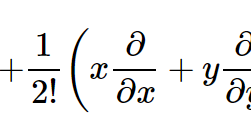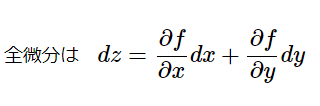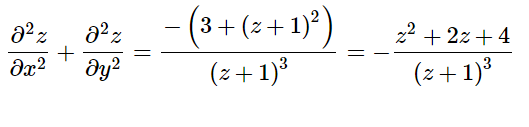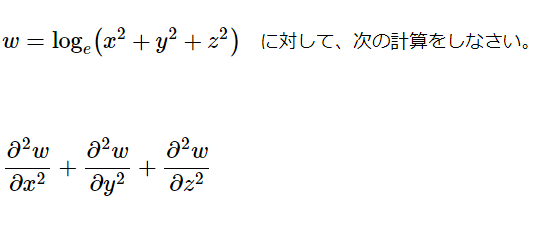ここで勉強すれば数学検定１級の壁は超えられるか。

[math]\sin ^{-1}2x\left( -\dfrac {1}{2}\leqq x\leqq \dfrac {1}{2}\right)[/math]　をマクローリン展開して[math]x^{3}[/math]の係数を求める。

[math]f\left( x\right) =\sin ^{-1}x[/math]　とおくと

[math]f'\left( x\right) =\dfrac {1}{\sqrt {1-x^{2}}}=\left( 1-x^{2}\right) ^{-\dfrac {1}{2}}[/math]

[math]f''\left( x\right) =\dfrac {d}{dx}\left( 1-x^{2}\right) ^{-\dfrac {1}{2}}=-\dfrac {1}{2}\left( -2x\right) \left( 1-x^{2}\right) ^{-\dfrac {3}{2}}[/math]

[math]f^{\left( 3\right) }\left( x\right) =\dfrac {d}{dx}x\left( 1-x^{2}\right) ^{-\dfrac {3}{2}}=\left( 1-x^{2}\right) ^{-\dfrac {3}{2}}+3x^{2}\left( 1-x^{2}\right) ^{-\dfrac {5}{2}}[/math]

したがって

[math]f^{\left( 3\right) }\left( 0\right) =1[/math]

マクローリン展開のｘの３乗の項は

[math]\dfrac {1}{3!}\left( 2x\right) ^{3}=\dfrac {4}{3}x^{3}[/math]　

[math]\dfrac {4}{3}[/math]・・・の答え