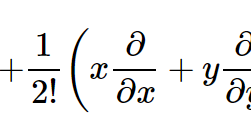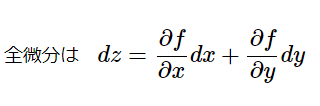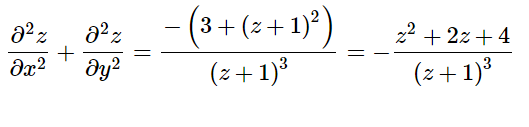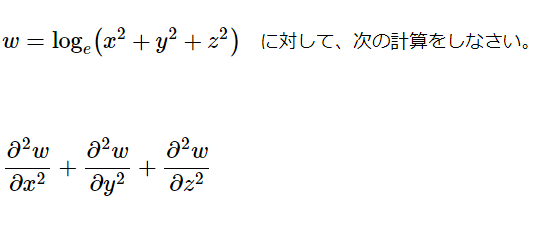ここで勉強すれば数学検定１級の壁は超えられるか。

 

 

[math]x^{2}+y^{2}+z^{2}+2x+2y+2z=0[/math]　のとき

[math]\dfrac {\partial ^{2}z}{\partial ^{2}x^{2}}+\dfrac {\partial ^{2}z}{\partial ^{2}y^{2}}[/math]　をｚの式で表す。

 

 

 

 

 

 

 [math]x^{2}+y^{2}+z^{2}+2x+2y+2z=0[/math]をｘで偏微分して２で割ると

 

 

 

[math]x+z\dfrac {\partial z}{\partial x}+1+\dfrac {\partial z}{\partial x}=0[/math]・・・①

 

 

式を変形すると

 

 

 

[math]\dfrac {\partial z}{\partial x}=-\dfrac {x+1}{z+1}[/math]・・・②

 

 

①の式を再度ｘで偏微分すると

 

 

[math]1+z\dfrac {\partial z}{\partial x}+\left( z+1\right) \dfrac {\partial ^{2}z}{\partial x^{2}}=0[/math]・・・③

 

 

同様に[math]\dfrac {\partial ^{2}z}{\partial ^{2}x^{2}}+\dfrac {\partial ^{2}z}{\partial ^{2}y^{2}}[/math]　をｙで偏微分すると

 

 

[math]y+z\dfrac {\partial z}{\partial y}+1+\dfrac {\partial z}{\partial y}=0[/math]・・・④

 

 

 

④を変形すると

 

 

[math]\dfrac {\partial z}{\partial y}=-\dfrac {y+1}{z+1}[/math]・・・⑤

 

 

 

④の式を再度ｙで偏微分すると

 

 

 

[math]1+\left( \dfrac {\partial z}{\partial y}\right) ^{2}+\left( z+1\right) \dfrac {\partial ^{2}z}{\partial y^{2}}=0[/math]・・・⑥　

 

 

③＋⑥より

 

 

 

[math]2+\left( \dfrac {\partial z}{\partial x}\right) ^{2}+\left( \dfrac {\partial z}{\partial y}\right) ^{2}+\left( z+1\right) \left( \dfrac {\partial ^{2}z}{\partial x^{2}}+\dfrac {\partial ^{2}z}{\partial y^{2}}\right)=0[/math]　

 

 

式変形して

 

 

[math]\left( z+1\right) \left( \dfrac {\partial ^{2}z}{\partial x^{2}}+\dfrac {\partial ^{2}z}{\partial y^{2}}\right) =-2-\left( \dfrac {\partial z}{\partial x}\right) ^{2}-\left( \dfrac {\partial z}{\partial y}\right) ^{2}[/math]・・・⑦

 

 

②と⑤を使って

 

 

[math]\left( \dfrac {\partial z}{\partial x}\right) ^{2}+\left( \dfrac {\partial z}{\partial y}\right) ^{2}=\dfrac {x^{2}+y^{2}+2x+2y+2}{\left( z+1\right) ^{2}}=-\dfrac {z^{2}+2z-2}{\left( z+1\right) ^{2}}[/math]・・・⑧

 

 

 

⑧を⑦に代入して

 

 

[math]\dfrac {\partial ^{2}z}{\partial x^{2}}+\dfrac {\partial ^{2}z}{\partial y^{2}}=-\dfrac {z^{2}+2z+4}{\left( z+1\right) ^{3}}[/math]・・・答え

 

 

 

 

 

 

 

 

別解

 

 

[math]x^{2}+y^{2}+z^{2}+2x+2y+2z=0[/math]　を変形して 

 

[math]z^{2}+2z+\left( x^{2}+y^{2}+2x+2y\right) =0[/math]

 

 

２次方程式の解の公式より

 

 

[math]z=-1\pm \sqrt {1-x^{2}-y^{2}-2x-2y}[/math]・・・①

 

 

[math]\dfrac {\partial z}{\partial x}=\pm \dfrac {1}{2}\cdot \dfrac {-2x-2}{\sqrt {1-x^{2}-y^{2}-2x-2y}}=\pm \dfrac {-x-1}{\sqrt {1-x^{2}-y^{2}-2x-2y}}[/math]

 

 

[math]\dfrac {\partial ^{2}z}{\partial x^{2}}=\pm \left\{ \dfrac {-1}{\sqrt {1-x^{2}-y^{2}-2x-2y}}-\dfrac {1}{2}\cdot \dfrac {\left( -x-1\right) （-2x-2）}{\left( \sqrt {1-x^{2}-y^{2}-2x-2y}\right)^{3} }\right\}[/math]

 

 

 

 

[math]=\pm \dfrac {-\left( 1-x^{2}-y^{2}-2x-2y\right) -\left( x^{2}+2x+1\right) }{\left( \sqrt {1-x^{2}-y^{2}-2x-2y}\right) ^{3}}[/math]

 

 

 

[math]=\pm \dfrac {-\left( 2-y^{2}-2y\right) }{\sqrt {\left( 1-x^{2}-y^{2}-2x-2y\right) }^{3}}[/math]

 

 

 

同様に

 

 

 

[math]\dfrac {\partial z^{2}}{\partial y^{2}}=\pm \dfrac {-\left( 2-x^{2}-2x\right) }{\left( \sqrt {1-x^{2}-y^{2}-2x-2y}\right) ^{3}}[/math]　

 

 

 

[math]\dfrac {\partial ^{2}z}{\partial x^{2}}+\dfrac {\partial ^{2}z}{dy^{2}}=\pm \dfrac {-\left( 4-x^{2}-y^{2}-2x-2y\right) }{\left( \sqrt {1-x^{2}-y^{2}-2x-2y}\right) ^{3}}[/math]　

 

 

 

ここで①より

 

 

 

[math]z+1=\pm \sqrt {1-x^{2}-y^{2}-2x-2y}[/math]

 

 

 

[math]\left( z+1\right) ^{2}=1-x^{2}-y^{2}-2x-2y[/math]

 

 

 

[math]\left( z+1\right) ^{3}=\left( \sqrt {1-x^{2}-y^{2}-2x-2y}\right) ^{3}[/math]

 

 

 

したがって

 

 

 

[math]\dfrac {\partial ^{2}z}{\partial x^{2}}+\dfrac {\partial ^{2}z}{\partial y^{2}}=\dfrac {-\left( 3+\left( z+1\right) ^{2}\right) }{\left( z+1\right) ^{3}}=-\dfrac {z^{2}+2z+4}{\left( z+1\right) ^{3}}[/math]

 

 

 

[math]-\dfrac {z^{2}+2z+4}{\left( z+1\right) ^{3}}[/math]・・・答え