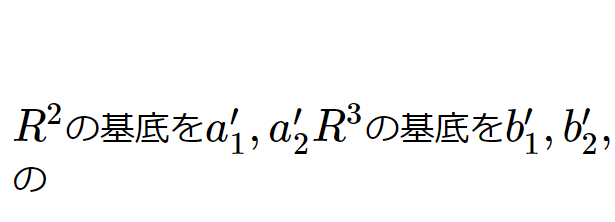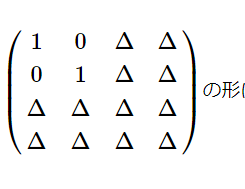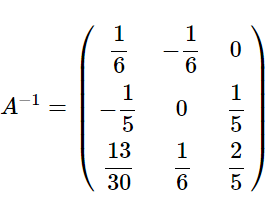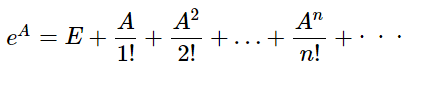ここで勉強すれば数学検定１級の壁は超えられるか。

Ａはｒ次正方行列、Ｄはｓ次正方行列、Ｂはｒ×ｓ、Ｏはｓ×ｒの０行列のとき

[math]\begin{vmatrix} A & B \\ O & D \end{vmatrix}=\left| A\right| \left| D\right|[/math]　が成り立つ。この式を使って求める。

[math]\begin{vmatrix} 0 & 0 & 0 & -2 & 2 \\ 0 & 0 & 0 & -4 & -1 \\ 2 & 7 & 6 & 8 & 3 \\ 9 & 5 & 1 & 4 & 7 \\ 7 & 3 & 8 & 5 & 9 \end{vmatrix}[/math]

２行を５行まで降ろす操作をする。

[math]=-\begin{vmatrix} 0 & 0 & 0 & -2 & 2\\ 2 & 7 & 6 & 8 & 3 \\ 9 & 5 & 1 & 4 & 7 \\ 4 & 3 & 8 & 5 & 9  \\ 0 & 0 & 0 & -4 & -1 \end{vmatrix}[/math]

次に１行を４行まで降ろす。

[math]=\begin{vmatrix} 2 & 7 & 6 & 8 & 3 \\ 9 & 5 & 1 & 4 & 7 \\ 4 & 3 & 8 & 5 & 9 \\ 0 & 0 & 0 & -2 & 2 \\ 0 & 0 & 0 & -4 & -1 \end{vmatrix}[/math]

ここで最初の公式を使うと

[math]=\begin{vmatrix} 2 & 7 & 6 \\ 9 & 5 & 1 \\ 4 & 3 & 8 \end{vmatrix}\begin{vmatrix} -2 & 2 \\ -4 & -1 \end{vmatrix}=-3600[/math]・・・答え

[math]\left( \left| A\right| \cdot \left| D\right| \right)[/math]