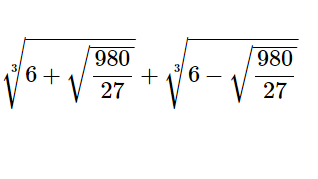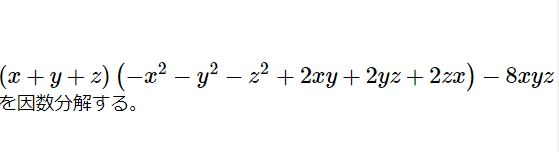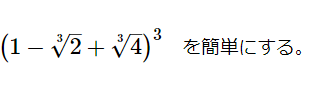ここで勉強すれば数学検定１級の壁は超えられるか。

次の連立方程式のうち、ｘ，ｙ，ｚがすべて実数であるものを求める。

[math]\begin{cases}xy^{2}z^{3}=\dfrac {12}{7}\\ x^{3}yz^{2}=-\dfrac {7}{11}\\ x^{2}y^{3}z=-\dfrac {11}{12}\end{cases}[/math]

３式を辺々ごとにかけると

[math]x^{6}y^{6}z^{6}=1[/math]

[math]x^{6}y^{6}z^{6}-1=\left( x^{2}y^{2}z^{2}-1\right) \left( x^{4}y^{4}z^{4}+x^{2}y^{2}z^{2}+1\right)=0[/math]

ｘｙｚは実数なので、

[math]x^{2}y^{2}z^{2}=1，xyz=\pm 1[/math]になる。

問題の各式を[math]x^{2}y^{2}z^{2}[/math]で割って

[math]\dfrac {z}{x}=\dfrac {12}{7},\dfrac {x}{y}=-\dfrac {7}{11}[/math]

[math]z=\dfrac {12}{7}x,y=-\dfrac {11}{7}x[/math]

[math]xyz=-\dfrac {11}{7}\times \dfrac {12}{7}x^{3}=-\dfrac {132}{49}x^{3}=\pm 1[/math]

[math]x=\mp \sqrt [3] {\dfrac {4}{132}},y=\pm \sqrt [3] {\dfrac {121}{84}},z=\mp \sqrt [3] {\dfrac {144}{77}}[/math]

[math]\left( x,y,z\right) ==\left( \pm \sqrt [3] {\dfrac {49}{132}},\mp \sqrt {3} {\dfrac {121}{84}},\pm \sqrt [3] {\dfrac {144}{77}}\right)[/math]　・・・答え