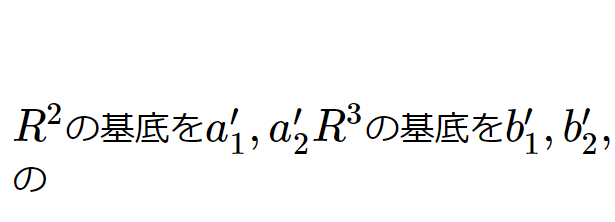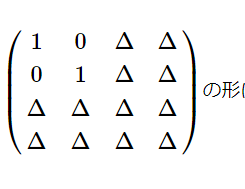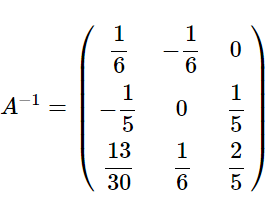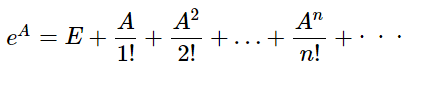ここで勉強すれば数学検定１級の壁は超えられるか。

 

次の行列がユニタリ行列となるように定数、a,b,c,dの値を定めなさい。ただし、iは虚数単位を表します。

 

[math]A=\begin{pmatrix} -\sqrt {2} & 1 & i \\ a & \sqrt {2}i & b \\ \sqrt {2} & c & d \end{pmatrix}[/math]　

 

 

 

 

 

 

 

ユニタリ行列は、各行ベクトル、各列ベクトルの大きさが１でかつお互いが直交する。

 

まず１列目の大きさより

 

 

[math]\left( \dfrac {1}{2}\begin{pmatrix} -\sqrt {2} \\　a \\　\sqrt {2} \end{pmatrix}\right) ^{2}=\dfrac {1}{4}\left( 2+a^{2}+2\right) =1[/math]

 

 

したがって、a＝０　になる。

 

 

第１行と２行の内積より

 

 

[math]\left( -\sqrt {2},1,-i\right) \cdot \left( 0,\sqrt {2}i,b\right) =0+\sqrt {2}i-bi=0[/math]

 

 

[math]b=\sqrt {2}[/math]

 

 

第１行と３行の内積より

 

 

[math]\left( -\sqrt {2},1,-i\right) \cdot \left( \sqrt {2},c,d\right) =-2+c-di=0[/math]・・・①であるから

 

 

[math]c=m+ni,d=x+yi[/math]・・・②となる。

 

 

第３行の大きさより

 

 

[math]\begin{aligned}\cdot \\ \dfrac {1}{2}\left( \sqrt {2},c,d\right) \cdot \dfrac {1}{2}\left( \sqrt {2},c,d\right) =\dfrac {2+c^{2}+d^{2}}{4}=1\end{aligned}[/math]

 

 

[math]\left| c\right| ^{2}+\left| d\right| ^{2}=2[/math]・・・③

 

 

第２列の大きさより

 

 

[math]\dfrac {1}{2}\left( 1,\sqrt {2}i,c\right) \cdot \dfrac {1}{2}\left( 15\sqrt {2}i,c\right) =\dfrac {c^{2}+3}{4}=1[/math]

 

 

[math]\left| c\right| ^{2}=1[/math]・・・④

 

 

③と④より

 

 

[math]\left| c\right| ^{2}= \left| d\right| ^{2}=1[/math]・・・⑤

 

 

①と②と⑤より

 

 

[math]m+ni-\left( x+yi\right) i=\left( m+y\right) +i\left( n-x\right) =2[/math]　

 

より

 

[math]m+y=2,n-x=0[/math]

 

 

[math]m^{2}+n^{2}=1,x^{2}+y^{2}=1\Rightarrow n^{2}+\left( 2-m\right) ^{2}=1[/math]

 

 

[math]\begin{aligned}\\ m^{2}+n^{2}=n^{2}+\left( 2-m\right) ^{2}\Rightarrow m^{2}=\left( 2-m\right) ^{2}\end{aligned}[/math]

 

 

[math]0=-4m+4\Rightarrow m=1\Rightarrow n=0[/math]

 

 

[math]x^{2}+y^{2}=x^{2}+m^{2}=1\Rightarrow x=0\Rightarrow y=1[/math]

 

 

したがって

 

 

[math]c=1+0i,d=0+i[/math]

 

 

a,b,c,dをまとめると

 

 

[math]a=0,b=\sqrt {2},c=1,d=i[/math]・・・答え