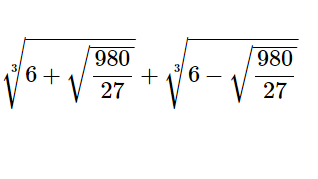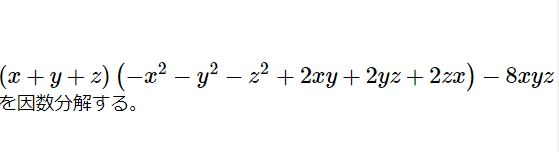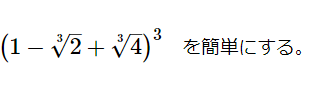ここで勉強すれば数学検定１級の壁は超えられるか。

[math]\left( x-2-\dfrac {3}{x}\right) ^{5}[/math]を展開したときの定数項を求める。

展開式の[math]x^{p}\left( -2\right) ^{q}\left( -\dfrac {3}{x}\right) ^{r}[/math]の係数は[math]\dfrac {5!}{p!q!r!}x^{p}\cdot \left( -2\right) ^{q}\left( -\dfrac {3}{x}\right) ^{r}[/math]・・・①　となる。

ｐ，ｑ，ｒはｐ＋ｑ＋ｒ＝５・・・②を満たす０または、正の整数で定数項という条件より

ｐ－ｒ＝０

ｐ＝ｒを②に代入する　２p＋ｑ＝５，[math]p=\dfrac {5-q}{2}\geqq 0[/math]から

ｑ＝１，３，５の３通りが考えられる。

・ｑ＝１のとき，ｐ＝ｒ＝２の場合

①より[math]\dfrac {5!}{2!1!2!}\left( -2\right) ^{1}\left( -3\right) ^{2}=-540[/math]

・ｑ＝３のとき、ｐ＝ｒ＝１

①より[math]\dfrac {5!}{1!3!1!}( -22^{3}\left( -3\right) ^{1}=480[/math]

・ｑ＝５のとき、ｐ＝ｒ＝０

①より[math]\dfrac {5!}{0!5!0!}\left( -2\right) ^{5}\left( -3\right) ^{0}=-32[/math]

したがって３つ場合をすべて加えると-540+480-32=-92

　　　-92　・・・答え