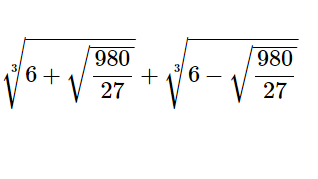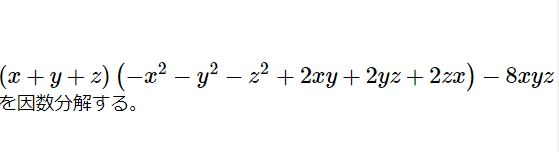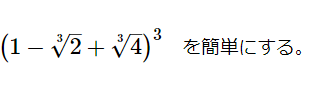ここで勉強すれば数学検定1級の壁は超えられるか。
3次方程式の解と係数の関係(式・方程式3)

[math]x^{3}-mx^{2}+nx-n=0[/math]
すべて解が正の整数になるような正の整数であるm,nを求める。
上の3次方程式の解をα,β,γとおくと解と係数の関係より
αβ+βγ+γα=n
αβγ=n
αβ+βγ+γα=αβγ
両辺をαβγで割ると
[math]\dfrac {1}{\alpha }+\dfrac {1}{\beta }+\dfrac {1}{\gamma }=1[/math]
この式を満たす正の整数のα,β,γの組み合わせを考える。
α≦β≦γとすると
[math]\left( \alpha ,\beta ,\gamma \right) =\left( 2,3,6\right) ,\left( 2,4,4\right) ,\left( 3,3,3\right)[/math]
α+β+γ=m
αβγ=n
からm,nを求める。
[math]\left( m,n\right) =\left( 11,36\right) ,\left( 10,32\right) ,\left( 9,27\right)[/math] ・・・答え
同じカテゴリー「数検1級の式・方程式など」の一覧
3次方程式3の解と係数の関係の応用編(式・方程式20)
[math]a^{3}+b^{3}+c^{3}-3abc=\left( a+b+c\right) \left( a^{2}+b^{2}+c^{2}-cb-bc-ca\right)[/ma […]
3重根から元の3次方程式を求める(式・方程式19)
[math]\sqrt [3] {6+\sqrt {\dfrac {980}{27}}}+\sqrt [3] {6-\sqrt {\dfrac {980}{27}}}[/math] & […]
x,y,zに関する式の因数分解(式・方程式18)
[math]\left( x+y+z\right) \left( -x^{2}-y^{2}-z^{2}+2xy+2yz+2zx\right) -8xyz[/math] を因 […]
無理数を含んだ式の展開(式・方程式17)
[math]\left( 1-\sqrt [3] {2}+\sqrt [3] {4}\right) ^{3}[/math] を簡単にする。 &n […]
x,y,zに関する3次式の因数分解(式・方程式16)
[math]xy\left( x^{2}-y^{2}\right) +yz\left( y^{2}-z^{2}\right) +zx\left( z^{2}-x^{2}\r […]