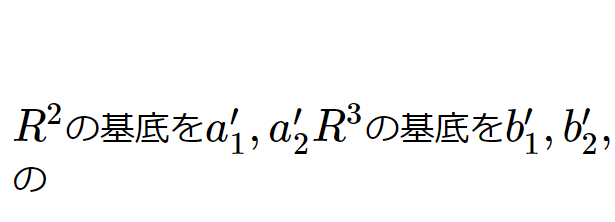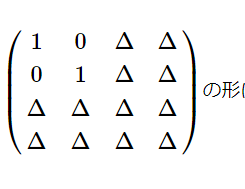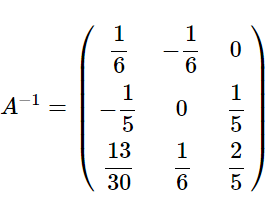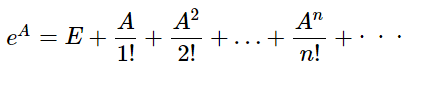ここで勉強すれば数学検定１級の壁は超えられるか。

 

$\begin{cases}2x+y+az=2a\\ x+ay-2z=2\\ x+2y-z=1\end{cases}$

 

 

①　この連立方程式を行列で表したとき、係数行列と拡大係数行列の階数が異なるような定数aを求める。

 

 

係数行列と拡大係数行列の階数が異なる場合は、連立方程式の解が不能の場合に該当する。

 

 

拡大行列のランクは　$\begin{pmatrix} 2 & 1 & a & 2a \\ 1 & a & -2 & 2 \\ 1 & 2 & -1 & 1 \end{pmatrix}$で

 

 

 

その小行列は　$\begin{pmatrix} 2 & 1 & a \\ 1 & a & -2 \\ 1 & 2 & -1 \end{pmatrix}=-2a^{2}+6a-7=-2\left( a-\dfrac {3}{2}\right) ^{2}-\dfrac {5}{2}\neq 0$

 

 

となって、拡大係数行列の階数は３になる。

 

 

一方、係数行列A　$\begin{pmatrix} 2 & 1 & a \\ 1 & a & -2 \\ 1 & 2 & -1 \end{pmatrix}$

 

 

でその小行列式$\begin{vmatrix} 2 & 1 \\ 1 & 2 \end{vmatrix}=4-1=3\neq 0$　なので、階数は２以上になる。したがって、係数行列が拡大係数行列の階数３にならない条件は

 

 

$\left| A\right| =\begin{vmatrix} 2 & 1 & a \\ 1 & a & -2 \\ 1 & 2 & -1 \end{vmatrix}=-a^{2}+7=0$

 

 

 

$a=\pm \sqrt {7}$のとき、連立方程式の解は不能になる。

 

 

 

$a=\pm \sqrt {7}$・・・①の答え

 

 

 

 

 

② 

①で求めた２つのaの値　$a_{1},a_{2}$　（ただし　$a_{1} <a_{2}$）に対して、連立方程式の３つの解であるｘ，ｙ，ｚの和の値が最大となるaの値を求める。

 

 

aの範囲が($-\sqrt {7}<a<\sqrt {7}$）になる。クラメールの公式からx,y,zを求める。

 

 

$x=\dfrac {\begin{vmatrix} 2a & 1 & a \\ 2 & a & -2 \\ 1 & 2 & -1 \end{vmatrix}}{\left| A\right| }=\dfrac {-3a^{2}+12a}{7-a^{2}}$

 

 

$y=\dfrac {\begin{vmatrix} 2 & 2a & a \\ 1 & 2 & -2 \\ 1 & 1 & - \end{vmatrix}_{1}}{\left| A\right| }=\dfrac {-3a}{7-a^{2}}$

 

 

$z=\dfrac {\begin{vmatrix} 2 & 1 & 2a \\ 1 & a & 2 \\ 1 & 2 & 1 \end{vmatrix}}{\left| A\right| }=\dfrac {-2a^{2}+6a-1}{7-a^{2}}$

 

 

よって

 

 

$x+y+z=\dfrac {-5a^{2}+15a-7}{7-a^{2}}=f\left( a\right)$　とおくと

 

 

$f\left( a\right) =\dfrac {5a^{2}-15a+7}{a^{2}-7}$

 

 

$\dfrac {df(a)}{da}=\dfrac {\left( 10a-15\right) \left( a^{2}-7\right) -\left( -5a^{2}+15a-7\right) \cdot 2a}{\left( a-7\right) ^{2}}$

 

 

$=\dfrac {15a^{2}-84a+105}{\left( a-7\right) ^{2} }$

 

 

$\dfrac {df(a)}{da}=0=\dfrac {15a^{2}-8a+105}{ \left(a-7\right) ^{2}}$となるのは、$a=\dfrac {14\pm \sqrt {21}}{5}=3.72,1.88$

 

 

 

ｆ（a）の増減表

a	・・・・・	１．８８	・・・・・	√７（２．６・・・）
f´(a)	＋	０	－	－
f(a)	／	極大（最大値）	＼	-∞

 

 

$-\sqrt {7}<a<\sqrt {7}$の範囲より、a=3.72は範囲の外である。

 

 

したがって、極大値をとるaの値は上の増減表より

 

 

$a=\dfrac {14-\sqrt {21}}{5}$となりかつ範囲内で最大値になる。

 

 

 

②の答え

 

$a=\dfrac {14-\sqrt {21}}{5}$のときに　x＋ｙ＋ｚは最大値をとる。