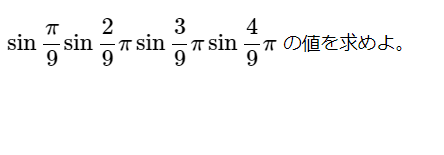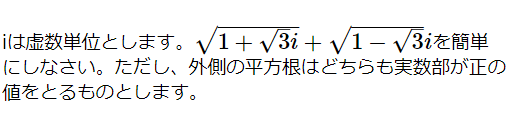ここで勉強すれば数学検定１級の壁は超えられるか。

複素数全体の部分集合

 

[math]A=\{ e^{\dfrac {1}{12}n\pi i }[/math]｜ｎ＝１，２，３・・・，１２｝

 

[math]B=\{ e^{\dfrac {5}{12}n\pi i }[/math]｜ｎ＝１，２，３・・・，１０｝

 

ただし、ｎは自然数の底，iは虚数の単位を表す。

 

 

 

①和集合A∪Bの要素の個数を求める。

 

②共通部分A∩Bの要素の個数を求める。

 

 

 

 

 

 

[math]A=\left\{ e^{\dfrac {7}{12}\pi i},e^{\dfrac {14}{12}\pi i},e^{\dfrac {21}{12}\pi i} ,\ldots ,e^{\dfrac {84}{12}\pi i}\right\}[/math]

 

 

 

[math]B=\left\{ e^{\dfrac {5}{12}\pi i},e^{\dfrac {10}{12}\pi i},e^{\dfrac {15}{12}\pi i},\ldots ,e^{\dfrac {50}{12}\pi i}\right\}[/math]

 

 

 

集合Aと集合Bをそれぞれ７ｎと５ｎをそれぞれ２４で割ったあまりの一致からA∩Bを求める。

 

 

 

　　　　　　７ｎ　　　mod24         ５ｎ 　              mod24

ｎ＝１             ７　　　　　７　　　　   ５　　　　　５

ｎ＝２　　　１４　　　　１４　　　　１０　　　　　１０

ｎ＝３　　　２１　　　　２１　　　　１５　　　　　１５

ｎ＝４　　　２８　　　　 ４　　　　  ２０　　　　　２０

ｎ＝５　　　３５　　　　１１　　　　２５　　　　 　   １

ｎ＝６　　　４２　　　　１８　　　　３０　　　　　　６

ｎ＝７　　　４９　　　　　１　　　　３５　　　　　１１

ｎ＝８　　　５６　　　　　８　　　　４０　　　　　１６

ｎ＝９　　　６３　　　　１５　　　　４５　　　　　２１

ｎ＝１０　　７０　　　　２２　　　　５０　　　　　　２

ｎ＝１１　　７７　　　　  ５　　　　

ｎ＝１２　　８４　　　　１２

 

 

 

２４で割った余りが共通なのは、２１，１１，１，１５，５の５つの点になる。

 

 

したがって、N（A∩B)＝５となる。

 

 

 

N（A∪B）＝N（A)＋N(B)－N（A∩B)＝１２＋１０－５＝１７

 

 

 

１７・・・①の答え

５・・・②の答え