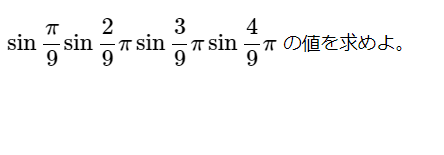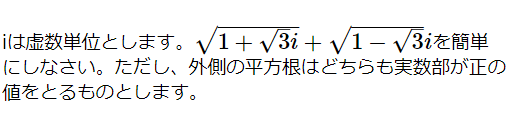ここで勉強すれば数学検定１級の壁は超えられるか。

$\sin \dfrac{\pi }{9}    \sin \dfrac{2}{9}\pi     \sin \dfrac{3}{9}\pi     \sin \dfrac{4}{9}\pi$ の値を求めよ。

 

 

 

 

 

 

 

$\alpha =\cos \dfrac{2}{9}\pi +i\sin \dfrac{2}{9}\pi$とおくと

 

ド・モアブルの定理より

 

$\alpha ^{9}=\left( \cos \dfrac{2\pi }{9}+i\sin \dfrac{2\pi }{9}\right) ^{9}=1$

 

$\alpha ^{9}-1=\left( \alpha -1\right) \left( \alpha ^{8}+\alpha ^{7}+\ldots +\alpha ^{2}+\alpha +1\right) =0$となる。

 

$\alpha \neq 1$より

 

$1+\alpha +\alpha ^{2}+\alpha ^{3}+\alpha ^{4}+\alpha ^{5}+\alpha ^{6}+\alpha ^{7}+\alpha ^{8}=0$が成り立つ。

 

 

ｎ＝１,２,３,４,５,６,７,８に対して、ド・モアブルの定理より

 

$\left( \alpha ^{n}\right) ^{9}=\left( \cos \dfrac{2n\pi }{9}+i\sin \dfrac{2n\pi }{9}\right) ^{9}=1$なので

 

よって、$\alpha ,\alpha ^{2},\alpha ^{3},\alpha ^{4},\alpha ^{5},\alpha ^{6},\alpha ^{7},\alpha ^{8}$　は方程式　$z^{9}=1$（zは複素数）

の１以外の異なる８つの解である。

 

したがって

 

８次方程式　$z^{8}+z^{7}+z^{6}+z^{5}+z^{4}+z^{3}+z^{2}+z+1=0$

の相違なる８つの解になる。

 

 

よって

$z^{8}+z^{7}+z^{6}+z^{5}+z^{4}+z^{3}+z^{2}+z+1=\left(z-\alpha \right) \left( z-\alpha ^{2}\right) \left( z-\alpha ^{3}\right) \left(z-\alpha ^{4}\right) \left( z-\alpha ^{5}\right) \left(z-\alpha ^{6}\right)\left( z-\alpha ^{7}\right) \left( z-\alpha ^{8}\right)$

・・・（１）

因数分解される。

 

 

次に

$\left| 1-\alpha ^{n}\right| ^{2}=\left( 1-\alpha ^{n}\right) \left( 1-\overline{\alpha }^{n}\right) =1-\left( \alpha ^{n}+\overline{\alpha }^{n}\right) +\left| \alpha ^{n}\right| ^{2}$

 

 

$=2-\left( \alpha ^{n}+\overline{\alpha }^{n}\right) =2-2\cos \dfrac{2n\pi }{9}=4\sin ^{2}\dfrac{n\pi }{9}$

・・・（２）

 

 

（１）はすべての複素数zに対して成り立つから、（１）式に　z＝１　とすると

$\left( 1-\alpha \right) \left( 1-\alpha ^{2}\right) \left( 1-\alpha ^{3}\right) \left( 1-\alpha ^{4}\right) \left( 1-\alpha ^{5}\right) \left( 1-\alpha ^{6}\right)\left( 1-\alpha ^{7}\right) \left( 1-\alpha ^{8}\right) =9$・・・（３）

 

 

 

n=1,2,3,4,5,6,7,8　のとき$\sin \dfrac{n\pi }{9} >0$だから

 

（２）より

 

$\sin \dfrac{n\pi }{9}=\dfrac{1}{2}\left| 1-\alpha ^{n}\right|$（n=1,2,3,4,5,6,7,8）

 

したがって

$\sin \dfrac{\pi }{9}\sin \dfrac{2}{9}\pi \sin \dfrac{3}{9}\pi \sin \dfrac{4}{9}\pi\sin \dfrac{5}{9}\pi \sin \dfrac{6}{9}\pi \sin \dfrac{7}{9}\pi \sin \dfrac{8}{9}\pi$

 

 

$=\left( \dfrac{1}{2}\right) ^{8}\left( 1-\alpha \right) \left( 1-\alpha ^{2}\right) \left( 1-\alpha ^{3}\right) \left( 1-\alpha^{4} \right) \left( 1-\alpha^{5} \right) \left( 1-\alpha^{6} \right)  \left( 1-\alpha ^{7}\right) \left( 1-\alpha ^{8}\right)=\dfrac{9}{16\times 16}$

 

 

$\sin \dfrac{\pi }{9}=\sin \dfrac{8\pi }{9},\sin \dfrac{2\pi }{9}=\sin \dfrac{7\pi }{9},\sin \dfrac{3\pi }{9}=\sin \dfrac{6\pi }{9},\sin \dfrac{4\pi }{9}=\sin \dfrac{5\pi }{9}$より

 

 

（$\sin \dfrac{\pi }{9}\sin \dfrac{2}{9}\pi \sin \dfrac{3}{9}\pi \sin \dfrac{4}{9}\pi$）（$\sin \dfrac{\pi }{9}\sin \dfrac{2}{9}\pi \sin \dfrac{3}{9}\pi \sin \dfrac{4}{9}\pi$）= $\left( \dfrac{3}{16}\right) ^{2}$

 

 

$\sin \dfrac{\pi }{9}\sin \dfrac{2}{9}\pi \sin \dfrac{3}{9}\pi \sin \dfrac{4}{9}\pi=\dfrac{3}{16}$・・・答え