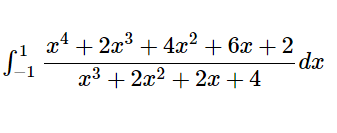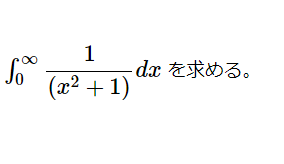ここで勉強すれば数学検定１級の壁は超えられるか。

[math]\int ^{\infty }_{0}\dfrac {1}{\left( x^{2}+1\right) ^{4}}dx[/math] を求める。　

[math]x=\tan \theta \Rightarrow x^{2}+1=\dfrac {1}{\cos ^{2}\theta }    ,           dx=\dfrac {1}{cos^{2}\theta }[/math]　

x:0→∞　            θ：0→[math]\dfrac {\pi }{2}[/math]

[math]\int ^{\infty }_{0}\dfrac {1}{\left( x^{2}+1\right) ^{4}}dx=\int ^{\dfrac {\pi }{2}}_{0}\dfrac {\cos ^{8}\theta }{\cos ^{2}\theta }d\theta[/math]

[math]=\int ^{\dfrac {\pi }{2}}_{0}\cos ^{6}\theta d\theta =\dfrac {5}{6}\cdot \dfrac {3}{4}\cdot \dfrac {1}{2}\cdot \dfrac {\pi }{2}=\dfrac {5}{32}\pi[/math]・・・答え

参考事項

[math]I_{n}=\int ^{\dfrac {\pi }{2}}_{0}\cos ^{n}\theta d\theta[/math]

ｎが偶数のとき

[math]I_{n}=\dfrac {n-1}{n}\cdot \dfrac {n-3}{n-2}-\cdot \ldots \dfrac {1}{2}\cdot \dfrac {\pi }{2}[/math]

ｎが奇数のとき

[math]I_{n}=\dfrac {n-1}{n}\cdot \dfrac {n-3}{n-2}-\ldots \dfrac {6}{7}\cdot \dfrac {4}{5}\cdot \dfrac {2}{3}[/math]