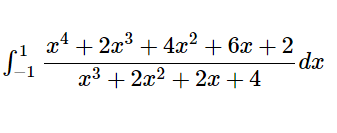ここで勉強すれば数学検定１級の壁は超えられるか。

①　次の不定積分を求める、ただし　（[math]-\dfrac {\pi }{2}\leqq \sin ^{-1}x\leqq \dfrac {\pi }{2}[/math]）を条件とする。

　　[math]\int \sin ^{-1}2xdx[/math]

②　ｘｙ平面のグラフで　[math]sin^{-1}2x\left( -\dfrac {1}{2}\leqq x\leqq \dfrac {1}{2}\right)[/math]とｘ軸、および２直線　　　[math]x=-\dfrac {1}{2},x=\dfrac {\sqrt {3}}{4}[/math]で囲まれた部分の面積を求めなさい。

①

[math]\int \sin ^{-1}2xdx=\int \left( x\right) '\sin ^{-1}2xdx[/math]

[math]=x\sin ^{-1}2x-\int x\cdot \left( \sin ^{-1}2x\right) ^{'}dx=x\sin ^{-1}2x-\int \dfrac {2x}{\sqrt {1-4x^{2}}}dx[/math]

[math]=x\sin ^{-1}2x-\int \dfrac {\left( 1-4x^{2}\right) '}{\sqrt {1-4x^{2}}}\cdot \left( -\dfrac {1}{4}\right) dx=x\sin ^{-1}2x+\dfrac {1}{4}\int \left( 1-4x^{2}\right) '\left( 1-4x^{2}\right) ^{-\dfrac {1}{2}}dx[/math]

[math]=x\sin ^{-1}2x+\dfrac {1}{4}\cdot 2\cdot \left( 1-4x^{2}\right) ^{\dfrac {1}{2}}+C=x\sin ^{-1}2x+\dfrac {\sqrt {1-4x^{2}}}{2}+C[/math]

[math]x\sin ^{-1}2x+\dfrac {\sqrt {1-4x^{2}}}{2}+C[/math]・・・①の答え

②

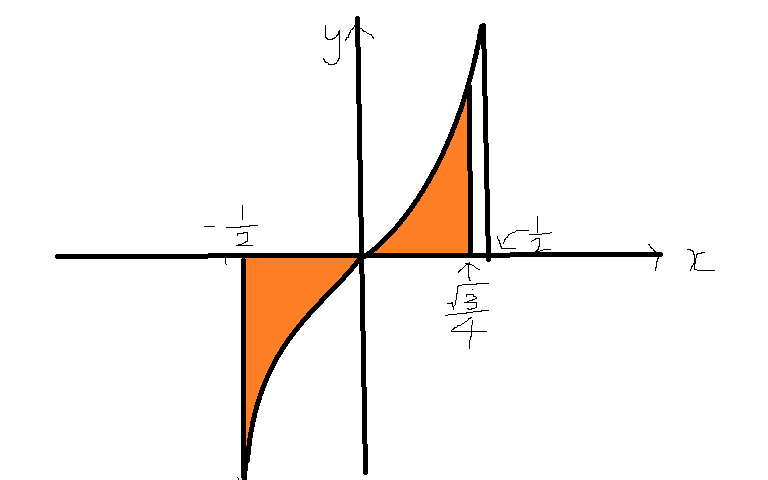
[math]y=\sin ^{-1}2x\Rightarrow 2x=\sin y\Rightarrow x=\dfrac {\sin y}{2}[/math]　上の図の色のついた部分が求める面積Sとなるので

[math]S=-\int ^{0}_{-\dfrac {1}{2}}\sin ^{-1}2xdx+\int ^{\dfrac {\sqrt {3}}{4}}_{0}\sin ^{-1}2xdx[/math]

[math]=-\left[ x\sin ^{-1}2x+\dfrac {\sqrt {1-4x^{2}}}{2}\right] ^{0}_{-\dfrac {1}{2}}+\left[ x\sin ^{-1}2x+\dfrac {\sqrt {1-4x^{2}}}{2}\right] ^{\dfrac {\sqrt {3}}{4}}_{0}[/math]

[math]=-\left\{ \dfrac {1}{2}-\left( -\dfrac {1}{2}\sin \left( -1\right) \right) \right\} +\left\{ \left( \dfrac {\sqrt {3}}{4}\sin ^{-1}\dfrac {\sqrt {3}}{2}+\dfrac {\sqrt {1-\dfrac {3}{4}}}{2}\right) -\dfrac {1}{2}\right\}[/math]

[math]=-\left( \dfrac {1}{2}+\dfrac {1}{2}\left( -\dfrac {\pi }{2}\right) \right) + \left( \dfrac {\sqrt {3}}{4}\cdot \dfrac {\pi }{3}+\dfrac {1}{4}-\dfrac {1}{2}\right) =\dfrac {3+\sqrt {3}}{12}\pi -\dfrac {3}{4}[/math]

[math]\dfrac {3+\sqrt {3}}{12}\pi -\dfrac {3}{4}[/math]・・・②の答え