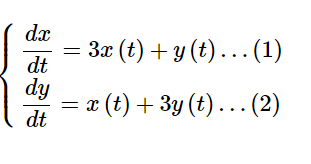ここで勉強すれば数学検定１級の壁は超えられるか。

 

次の微分方程式で、初期条件がx=１のとき、y=1/2　を満たすものを求める。

 

 

[math]\left( 3x-y\right) \dfrac {dy}{dx}=2x[/math]

 

 

 

 

 

この微分方程式を変形すると、

 

 

[math]\dfrac {dy}{dx}=\dfrac {2x}{3x-y}=\dfrac {2}{3-\dfrac {y}{x}}[/math]

 

 

[math]\dfrac {y}{x}=u[/math]とおくと、[math]y=ux+\dfrac {dy}{dx}=\dfrac {du}{dx}x+u[/math]

 

 

 

[math]\dfrac {du}{dx}=\dfrac {2}{3-u}-u=\dfrac {u^{2}-3u+2}{3-u}=\dfrac {\left( u-1\right) \left( u-2\right) }{3-u}[/math]

 

 

[math] \dfrac {3-u}{\left( u-1\right) \left( u-2\right) }du=\dfrac {1}{x}dx[/math]

 

 

 

[math]\left( \dfrac {1}{u-2}-\dfrac {2}{u-1}\right) du=\dfrac {1}{x}dx[/math]

 

 

両辺を積分すると

 

 

[math]\log _{e}\left( u-2\right) -2\log _{e}\left( u-1\right) du=\log _{e}x+C[/math]（Ｃは積分定数）

 

 

[math]\dfrac {u-2}{\left( u-1\right) ^{2}}=Ax[/math]（[math] A＝e^{Ｃ}[/math]）

 

 

 

両辺をxで割ると

 

 

 

[math]\dfrac {x\left( u-2\right) }{x^{2}\left( u-1\right) ^{2}}=A[/math]

 

 

 

[math]y-2x=A\left( y-x\right) ^{2}[/math]　　　　( y=uxより)

 

 

 

初期条件より

 

 

[math]x=0,y=\dfrac {1}{2}\Rightarrow \dfrac {1}{2}＝\dfrac {A}{4}\Rightarrow A=2[/math]

 

 

 

[math]y-2x=2\left( y-x\right) ^{2}[/math]・・・答え