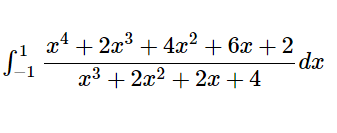ここで勉強すれば数学検定1級の壁は超えられるか。
積分3の解説

[math]\int ^{1}_{-1}\sqrt {\dfrac {1+x}{1-x}}dx[/math]の広義積分を計算する。
本当は広義積分をしなければならないが、答えが同じになるので、普通の積分のやり方で解く。
(1次試験は答えのみ記入するため、1問当たりの時間短縮が目的)
[math]\sqrt {1-x}=t[/math] とおくと
[math]\sqrt {1-x}=t\Rightarrow 1-x=t^{2}\Rightarrow -dx=2tdt[/math]
[math]x: -1\rightarrow 1,t:\sqrt2 \rightarrow 0[/math]
また、[math]\sqrt {1+x}=\sqrt {2-t^{2}}\Rightarrow \sqrt {\dfrac {1+x}{1-x}}=\dfrac {\sqrt {2-t^{2}}}{t}[/math]
したがって、
[math]\int ^{1}_{-1}\sqrt {\dfrac {1+x}{1-x}}dx=\int ^{0}_{\sqrt2}\dfrac {\sqrt {2-t^{2}}}{t}\left( -2t\right) dt[/math]
[math]=\int ^{0}_{\sqrt2}-2\sqrt {2-t^{2}}dt=2\int ^{\sqrt2}_{0}\sqrt {2-t^{2}}dt[/math]
[math]=2\times \dfrac {1}{2}\left[ t\sqrt {2-t^{2}}+2\sin ^{-1}\dfrac {t}{\sqrt {2}}\right] ^{\sqrt {2}}_{0}[/math]
[math]=\left\{ \left( 0+2\cdot \dfrac {\pi }{2}\right) -\left( 0+0\right) \right\} =\pi[/math]・・・答え
別解
[math]\int ^{1}_{-1}\sqrt {\dfrac {1+x}{1-x}}dx[/math]
ここで [math]\sqrt {\dfrac {1+x}{1-x}}=\dfrac {\sqrt {1+x}}{\sqrt {1-x}}\times \dfrac {\sqrt {1+x}}{\sqrt {1+x}}=\dfrac {1+x}{\sqrt {1-x^{2}}}[/math]
よって
[math]\int ^{1}_{-1}\sqrt {\dfrac {1+x}{1-x}}dx=\int ^{1}_{-1}\dfrac {1}{\sqrt {1-x^{2}}}dx+\int ^{1}_{-1}\dfrac {x}{\sqrt {1-x^{2}}}dx[/math]
[math]=\left[ \sin ^{-1}\right] ^{1}_{-1}-\left[ \dfrac {1}{\sqrt {1-x^{2}}}\right] ^{1}_{-1}[/math]となるから
[math]=\dfrac {\pi }{2}-\left( -\dfrac {\pi }{2}\right) -0= \pi[/math]
答 [math]\pi[/math]