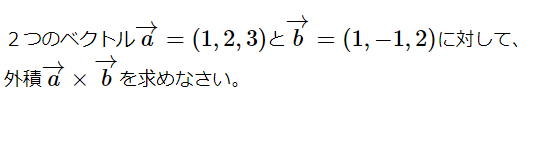ここで勉強すれば数学検定1級の壁は超えられるか。
接平面を求める(ベクトル7)

[math]z=\log _{e}\left( x^{2}+xy+3y^{2}\right)[/math]
[math]\left( -1,1,\log _{e}3\right)[/math]における接平面の方程式を求める。
接平面の法線ベクトルは
[math]\dfrac {\partial z}{\partial x}=\dfrac {2x+y}{x^{2}+xy+3y^{2}},\dfrac {\partial z}{\partial y}=\dfrac {x+6y}{x^{2}+xy+3y^{2}}[/math]
[math]\left( \dfrac {\partial z}{\partial x},\dfrac {\partial z}{\partial y},-1\right) =\left( -\dfrac {1}{3},\dfrac {5}{3},-1\right)[/math]となる。
したがって、接平面の方程式は
[math]-1\times \left( x+1\right) +5\left( y-1\right) -3\left( z-\log _{e}3\right) =0[/math]
[math]x-5y+3z=-6+3\log _{e}3[/math]・・・の答え
同じカテゴリー「数検1級のベクトル」の一覧
ベクトル3重積のヤコビの等式
(1)次の式を証明せよ [math]a\times\left( b\times c\right)[/math] [math]=\left( a\cdot c\right) b-\left( a\cdo […]
空間にある平行でない2直線の最短距離の求め方(ベクトル16)
[math]l_{1},l_{2}[/math]の外積の絶対値と同じ面積の平行四辺形を上底面、底面と考えて、dを高さとする平行六面体と上底面と底面が同じで[math](x_{1}-x_{2})[/ma […]
2つの外積の計算方法(ベクトル15)
2つのベクトル[math]\overrightarrow {a}=\left( 1,2,3\right)[/math]と[math]\overrightarrow {b}=\left( […]
直線を一次変換したときの方程式(ベクトル14)
xyz空間の1次変換f:[math]\begin{pmatrix} x \\ y \\ z \end{pmatrix}\rightarrow \begin{pmatrix} 1 & […]
ベクトルがつくる平行四辺形の面積(ベクトル13)
空間内の4点O(0,0,0),A(-1,-2,-1),B(1,-2,-1),C(2,-1,3)である。 ① 線分OA,OBを隣り合う2辺にもつ平行四辺形の面積 […]