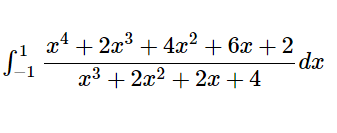ここで勉強すれば数学検定１級の壁は超えられるか。

[math]\int ^{1}_{-1}\dfrac {x^{4}+2x^{3}+4x^{2}+6x+2}{x^{3}+2x^{2}+2x+4}dx[/math]　を計算する。

[math]\int ^{1}_{-1}\dfrac {x^{4}+2x^{3}+4x^{2}+6x+2}{x^{3}+2x^{2}+2x+4}dx=\int ^{1}_{-1}\left( x+\dfrac {2x^{2}+2x+2}{x^{3}+2x^{2}+2x+4}\right) dx[/math]

ここで

[math]\left( x^{3}+2x^{2}+2x+4\right) '=3x^{2}+4x+2[/math]　

[math]x^{3}+2x^{2}+2x+4=\left( x+2\right) \left( x^{2}+2\right)[/math]　であることを確認する。

[math]=\int ^{1}_{-1}xdx+\int ^{1}_{-1}\dfrac {\left( x^{3}+2x^{2}+2x+4\right) '-\left( x^{2}+2x\right) }{x^{3}+2x^{2}+2x+4}dx[/math]

[math]=0+\left[ \log _{e}\left( x^{3}+2x^{2}+2x+4\right) \right] ^{1}_{-1}-\int ^{1}_{-1}\dfrac {x}{x^{2}+2}dx[/math]

[math]=\log _{e}9-\log _{e}3-\dfrac {1}{2}\left[ \log _{e}\left( x^{2}+2\right) \right] ^{1}_{-1}[/math]

[math]=2\log_{e}3-loge_{e}3-0=\log _{e}3[/math]

[math]\log _{e}3[/math]・・・答え