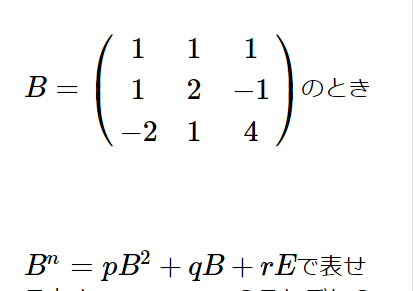ここで勉強すれば数学検定１級の壁は超えられるか。

 

 

次の問いに答えなさい。

[math]\int ^{\dfrac {\pi }{2}}_{0}\sqrt {\tan x}dx[/math]

 

 

 

 

 

[math]\sqrt {\tan x}=t\Rightarrow \dfrac {1}{2\sqrt {\tan x}}\cdot \dfrac {dx}{\cos ^{2}x}=dt[/math]より、

 

 

 

[math]dx=\dfrac {2t}{t^{4}+1}dt　　　( \because \cos ^{2}x=\dfrac {1}{1+\tan ^{2}x}[/math]）

 

 

 

[math]\int _{0}\sqrt [\dfrac {\pi }{2}] {\tan x}dx=\int ^{\infty }_{0}\dfrac {2t^{2}}{t^{4}+1}dt=\int ^{\infty }_{-\infty }\dfrac {t^{2}}{t^{4}+1}dt[/math]  (偶関数でy軸について対称のグラフになる）

 

 

 

 

ここで　[math]f\left( z\right) =\dfrac {z^{2}}{z^{4}+1}[/math]　とおくと

 

 

[math] \left| z\right| \rightarrow \infty \Rightarrow \left| zf\left( z\right) \right| \rightarrow 0[/math]　なので

 

 

 

 

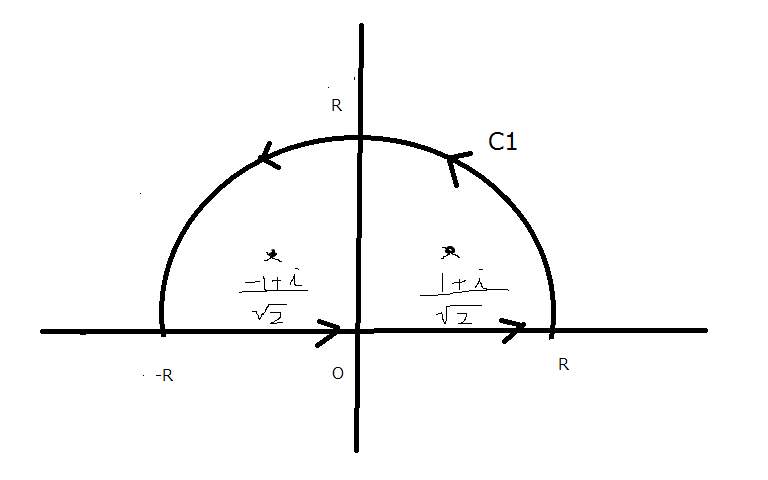
上図のような積分経路C1（ただしR→∞）

 

 

[math]\int ^{\infty }_{-\infty }\dfrac {t^{2}}{t^{4}+1}dt=\oint _{C_{1}}\dfrac {z^{2}}{z^{4}+1}dz[/math]となり留数定理が使える。

 

 

ｆ（ｚ）のC1内の特異点は　[math]e^{\dfrac {\pi }{4}i}=\dfrac {1+i}{\sqrt {2}},e^{\dfrac {3}{4}\pi i}=\dfrac {-1+i}{\sqrt {2}}[/math]になる。共に１位の極である。

 

この２つの留数を求める。

 

 

 

[math]f\left( z\right) =\dfrac {z^{2}}{z^{4}+1}=\dfrac {z^{2}}{\left\{ z-\left( \dfrac {1+i}{\sqrt {2}}\right) \right\} \left\{ z-\left( \dfrac {-1+i}{\sqrt {2}}\right) \right\} \left\{ z-\left( \dfrac {1-i}{\sqrt {2}}\right) \right\} \left\{ z-\left( \dfrac {-1-i}{\sqrt {2}}\right) \right\}}[/math]

 

 

だから求める留数は　　a＝（１＋i）/√２として

 

 

[math]R_{1}=\lim _{z\rightarrow a}\left( z-\dfrac {1+i}{\sqrt {2}}\right) f\left( z\right)=\dfrac {\dfrac {\left( 1+i\right) ^{2}}{2}}{\sqrt {2}\times \sqrt {2}\left( 1+i\right) \times \sqrt {2}i}=\dfrac {1-i}{4\sqrt {2}}[/math]

 

 

 

b＝（－１＋i）/√２とおいて

 

 

 

[math]R_{2}=\lim _{z\rightarrow b}\left( z-\dfrac {-1+i}{\sqrt {2}}\right) f\left( z\right) =\dfrac {\dfrac {\left( -1+i\right) ^{2}}{2}}{\left( -\sqrt {2}\right) \times \sqrt {2}\left( -1+i\right) ^{2}\times \sqrt {2}i}=\dfrac {-\left( 1+i\right) }{4\sqrt {2}}[/math]

 

 

したがって

 

 

[math]\oint _{C_{1}}\dfrac {z^{2}}{z^{4}+1}dz=2\pi i\left[ \dfrac {1-i}{4\sqrt {2}}-\dfrac {1+i}{4\sqrt {2}}\right] =\dfrac {\pi }{\sqrt {2}}[/math]・・・答え